Correspondence (mathematics)

In mathematics and mathematical economics, correspondence is a term with several related but not identical meanings.

In general mathematics, correspondence is an alternative term for a relation between two sets. Hence a correspondence of sets X and Y is any subset of the Cartesian product X×Y of the sets.

In algebraic geometry, a correspondence between algebraic varieties V and W is in the same fashion a subset R of V×W, which is in addition required to be closed in the Zariski topology. It therefore means any relation that is defined by algebraic equations. There are some important examples, even when V and W are algebraic curves: for example the Hecke operators of modular form theory may be considered as correspondences of modular curves.

However, the definition of a correspondence in algebraic geometry is not completely standard. For instance, Fulton, in his book on Intersection theory, uses the definition above. In literature, however, a correspondence from a variety X to a variety Y is often taken to be a subset Z of X×Y such that Z is finite and surjective over each component of X. Note the asymmetry in this latter definition; which talks about a correspondence from X to Y rather than a correspondence between X and Y. The typical example of the latter kind of correspondence is the graph of a function f:X→Y

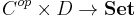In category theory, a correspondence from $C$ to $D$ is a functor $C^{op}\times D\to\mathbf{Set}$ . It is the "opposite" of a profunctor.

One-to-one correspondence is an alternate name for a bijection.

In von Neumann algebra theory, a correspondence is a synonym for a von Neumann algebra bimodule.

In economics, a correspondence between two sets A and B is a map f:A→P(B) from the elements of the set A to the power set of B. This is similar to a correspondence as defined in general mathematics (i.e., a relation,) except that the range is over sets instead of elements. However, there is usually the additional property that for all a in A, f(a) is not empty. In other words, each element in A maps to a non-empty subset of B; or in terms of a relation R as subset of A×B, R projects to A surjectively. A correspondence with this additional property is thought of as the generalization of a function, rather than as a special case of a relation, and is referred to in other contexts as a multivalued function.

An example of a correspondence in this sense is the best response correspondence in game theory, which gives the optimal action for a player as a function of the strategies of all other players. If there is always a unique best action given what the other players are doing, then this is a function. If for some opponent's strategy, there is a set of best responses that are equally good, then this is a correspondence.